

To correct for these effects, Ribbefor's relativistic impulse approximation (IA) will be employed to create scattering cross section differential in both energy and angle for each element. While this technique accounts for binding effects on the scattering angle, it excludes the Doppler broadening the Compton line undergoes because of the momentum distribution in each bound state.
#Compton effect recoil angle of electron free#
In its current model of Compton more » scattering, ITS corrects the differential Klein-Nishina cross sections (which assumes a stationary, free electron) with the incoherent scattering function, a function dependent on both the momentum transfer and the atomic number of the scattering medium. Compton scattering is the dominant photon interaction above 100 keV and below 5-10 MeV, with higher cutoffs occurring in lighter atoms. Monte Carlo simulations must therefore be both physically accurate and computationally efficient. Reducing these variations is heavily dependent on runtime. Unlike its deterministic counterpart, the Monte Carlo calculations of ITS do not require a memory-intensive meshing of phase space however, its solutions carry statistical variations. ITS performs analog photon tracking for energies between 1 keV and 1 GeV.
#Compton effect recoil angle of electron software#
The Integrated TIGER Series (ITS) is a software package that solves coupled electron-photon transport problems. Finally, it is concluded that the biggest factor in determining the rise time of the signal is not the dynamics of the Compton current, but is instead the conductivity. Moreover, these approximations are examined in the context of a high-altitude burst, and it is shown that in comparison to more complete models, the discrepancy between field amplitudes is roughly two to three percent and between rise-times, 10%. The neglect of this derivative improperly treats the backward-traveling wave. Additionally, legacy codes also neglect the more » radial derivative of the backward-traveling wave for computational efficiency. In using a Monte-Carlo description of scattering, two distributions of scattering angles are considered: Gaussian and a Gaussian with a single-scattering tail. Obliquity factor predictions are compared with Monte-Carlo models. Here, this previous analysis is extended to include the generation of the electromagnetic fields. A recent publication has examined this approximation in the context of the generated Compton current. The legacy codes developed for the modeling of EMP, multiple scattering of Compton electrons has typically been modeled by the obliquity factor. However, as the gamma energy increases and the Klein-Nishina becomes more peaked in the forward direction, skewness in the distribution causes greater disagreement between the obliquity factor and a more accurate model of multiple = , It is found that, in general, the obliquity factor is adequate for most situations. Here, the obliquity factor and Fokker-Planck finite-difference approaches are then compared in a fuller treatment, which includes the initial Klein-Nishina distribution of the electrons, and the momentum dependence of both drag and scattering. It is demonstrated that the obliquity factor does not correctly capture this skewness, but the Monte-Carlo and Fokker-Planck finite-difference approaches do.
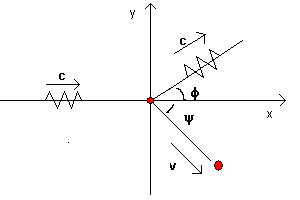
Because of the Doppler effect, skewness occurs in the distribution. The simplified problem is solved three ways: the obliquity factor, Monte-Carlo, and Fokker-Planck finite-difference. A simplified model problem, which correctly captures cyclotron motion, Doppler shifting due to the electron motion, and multiple scattering is first considered. The validity of this approach is examined here. Multiple scattering has historically been treated in EMP modeling through the obliquity factor.


 0 kommentar(er)
0 kommentar(er)
